Question

I got the answer just need to check up with someone

Answer 1

Concept:

The volume of the triangular pyramid will be calculated using the formula below

`\begin{gathered} V=(1)/(3)* base\text{ area}* height \\ \text{Height of the pyramid=H=15yd} \end{gathered}`

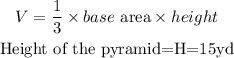
In this case, the base is a triangle...Therefore, the area of the base will be calculated using the formula below

`\begin{gathered} \text{Baes area=}(1)/(2)* base* height \\ \text{base of the triangle=b=5yd} \\ \text{height of triangle=h=12yd} \end{gathered}`

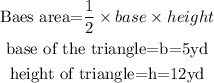
Step 1:

Calculate the area of the base using the formula above

`\begin{gathered} \text{Baes area=}(1)/(2)* base* height \\ \end{gathered}`

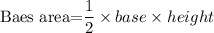
By substituting the values, we will have

`\begin{gathered} \text{Base area=}(1)/(2)* base* height \\ \text{Base area}=(1)/(2)*5yd*12yd \\ \text{Base area}=(60yd^2)/(2) \\ \text{Base area}=30yd^2 \end{gathered}`

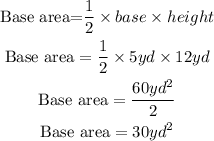
Step 2:

Calculate the volume of the triangular based pyramid using the formula below

`\begin{gathered} V=(1)/(3)* base\text{ area}* height \\ \text{Where,} \\ \text{Base area=30yd}^2 \\ \text{Height}=H=15yd \end{gathered}`

By substituting the values, we will have

`\begin{gathered} V=(1)/(3)* base\text{ area}* height \\ V=(1)/(3)*30yd^2*15yd \\ V=(450yd^3)/(3) \\ V=150yd^3 \end{gathered}`

Hence,

The volume of the triangular based pyramid is = 150 yd³