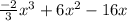Question

If f'(x) is (x-4)(4-2x) , what is f(x)?

Answer 1

we can apply some rules backwards

first
f'(x)=
(x-4)(-2x+4)
-2x^2+12x-16

we know that

`f'(rx^n)=rnx^(n-1)`
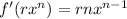
so therefor maybe
-2x^2=rnx^{n-1}
2=n-1
n=3
rn=-2
3r=-2
r=-2/3

one is

`(-2)/(3)x^3`
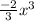
second part

12x
12x=
`rnx^(n-1)`
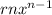
x^1, 1=n-1
n=2
rn=12
2r=12
r=6

`6x^2` is the second bit

last part
-16
-16x^0=
`rnx^(n-1)`
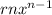
0=n-1
n=1

rn=-16
1r=-16
r=-16

-16x^1

so therfor f(x)=
`(-2)/(3)x^3+6x^2-16x`