Question

You want to obtain a sample to estimate a population mean. Based on previous evidence, you believe thepopulation standard deviation is approximately o = 72.7. You would like to be 95% confident that yourestimate is within 10 of the true population mean. How large of a sample size is required? Do not roundmid-calculation

Answer 1

The standard deviation is:

`s=72.7`

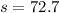
The confidence interval is 95%

You want to be confident that your estimate is within 10 of the true population mean, then you can use the next formula:

`ME=z\frac{s}{\sqrt[]{n}}`

Where ME is the marginal error, z is the z-score (for a confidence interval of 95% is 1.96), s is the standard deviation and n the sample size.

Then, by replacing the values:

`\begin{gathered} 10=1.96\frac{72.7}{\sqrt[]{n}} \\ 10*\sqrt[]{n}=1.96\frac{72.7}{\sqrt[]{n}}*\sqrt[]{n} \\ 10*\sqrt[]{n}=1.96*72.7 \\ \sqrt[]{n}=(1.96*72.7)/(10) \\ \sqrt[]{n}=14.2492 \\ \sqrt[]{n}^2=14.2492^2 \\ n=203.04 \end{gathered}`

Thus, you need a sample size of at least 204 people.