number is 'n'
square of a number means n^2
added to means plus or +
number trippled is 3n
result means equals or =
108 is 108
n^2+3n=108
minus 108 from both sides
n^2+3n-108=0
if want quadratic formula
in form
ax^2+bx+c=0
x=
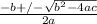
a=1
b=3
c=-108
x=

x=

x=

x=

x=
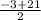
or x=

x=

or x=

x=9 or -12
the number is either 9 or -12