To get the possible length of segment AB from the triangle given, then we use the triangle inequality theorem.
The Triangle inequality theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side.
From this theorem, we sum the two sides given
Given:
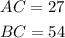
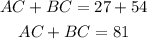
Applying the triangle inequality theorem, the sum of any 2 sides of a triangle must be greater than the measure of the third side.
This means AC + BC > AB
81 > AB. This also means AB < 81
From the options given, AB = 25 is not a possible value because adding it to side AC gives 52. Hence, when AB = 25, AB + AC < BC (52 < 54) and does not obey the triangle inequality theorem.
Also, AB < 27 or AB > 81 will not be a possible value.
Therefore, the expression for all possible lengths of segment AB of the triangle is
27 < AB < 81 as it will satisfy the triangle inequality theorem.