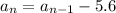Question

What is the recursive rule for the sequence -2.7 -8.3 -13.9 -19.5 -25.1

an= an+1+5.6
an=an+1-5.6
an=an-1-5.6
an=an-1+5.6

Answer 1

an=an-1-5.6 C

Explanation:

I took the quiz k12

Answer 2

Option C is correct

`a_n = a_(n-1)-5.6`

Explanation:

The recursive rule for the arithmetic sequence is given by:

`a_n = a_(n-1)+d` .....[1]

where,

`a_n` is the nth term and d is the common difference between two successive terms.

As per the statement:

-2.7 -8.3 -13.9 -19.5 -25.1

This sequence is an arithmetic sequence with first term -2.7 and common difference(d) = -5.6.

Since;

-8.3 -(-2.7) = -8.3 +2.7 = -5.6,

-13.9 -(-8.3) = -13.9+8.3= -5.6 and so on..

Substitute the value of d = -5.6 in [1] we have;

`a_n = a_(n-1)-5.6`

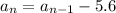
Therefore, recursive rule for the given sequence is,
`a_n = a_(n-1)-5.6`