Question

If a number is added to the numerator of 5/6 and twice as much is added to the denominator, the result is 3/5. Find the number.

Answer 1

We are given that a number is added to the numerator of 5/6. If "x" is the number then this can be written mathematically as:

`(5+x)/(6)`

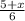
we also told that twice this number is added to the denominator, this can be written mathematically as:

`(5+x)/(6+2x)`

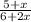
We are also told that the result of this operation of 3/5, therefore, we have:

`(5+x)/(6+2x)=(3)/(5)`

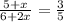
We get an equation with one variable. To solve this equation we will cross multiply the equation, like this:

`5(5+x)=3(6+2x)`

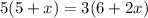
Now we will apply the distributive property on both parentheses:

`25+5x=18+6x`

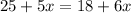
Now we subtract 6x from both sides:

`\begin{gathered} 25+5x-6x=18+6x-6x \\ 25-x=9 \end{gathered}`

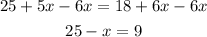
Now we subtract 25 from both sides:

`\begin{gathered} 25-25-x=18-25 \\ -x=-7 \end{gathered}`

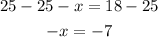
Now we multiply both sides by -1:

`x=7`

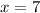
Therefore, the number is 16.

Let's replace the value of "x" in the expression: