The equation to calculate the volume for pyramids is:

For prisms is:
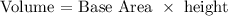
Cylinder is:
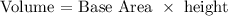
Cone:

Thus let's analyze the sentences:
1) Prism M and pyramid N have the same base area and the same height.
The equation of the volume is different, so they are not going to have the same volume.
2) Cylinder P and prism Q have the same height and the same base perimeter.
The same base perimeter is not a guarantee that they have the same base area. So the volumes are not equal too.
3) Cone Z has the same base area as cylinder Y, but its height is three times the height of cylinder Y.
Let's see if the base area is 'A' and the height of the cylinder is '3H':
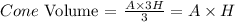
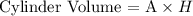
Thus the Cone Z and the cylinder Y will have the same volume!