Question

What is the domain of y=log5x

all real numbers less than 0
all real numbers greater than 0
all real numbers not equal to 0
all real numbers

Answer 1

The domain of the function y=log5x is all real numbers greater than zero since logarithms of negative numbers or zero are undefined.

Step-by-step explanation:

The domain of a logarithmic function, such as y = log5x, refers to the set of all possible x-values for which the function is defined. In the case of a logarithm, the domain consists of all positive real numbers, because the logarithm of a negative number or zero is undefined. Therefore, the domain of y = log5x is all real numbers greater than 0.

Answer 2

The correct option is 2.

Step-by-step explanation:

The given function is

`y=log5x`

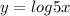
It is an logarithmic function. If a logarithmic function is defined as

`f(x)=log_a(bx)`

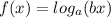
Where, a is base of log and b>0 is constant.

Then, the domain of the function is all real numbers greater than 0, because the logarithmic function is not defined for any negative number.

Since the given function is a logarithmic function, therefore the domain of the function is all real numbers not equal to 0.

`Domain=\x>0\`

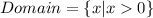
Therefore option 2 is correct.