Question

A pizza shop owner wishes to find the 95% confidence interval of the true mean cost of a large plain pizza. How large should the sample be if she wishes to be accurate to within $0.14? A previous study showed that the standard deviation of the price was $0.45. (Remember that the answer has to be a whole number.)

Answer 1

As per given by the question,

There are given that,

The confidence interval is 95%, standard deviation is $0.45, and the margine of error is $0.14.

Now,

From the confidence interval 95%,

Here,

`\alpha=0.05`

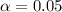
Because of according to the z-score table,

There are given that in the form of row and column.

Now,

The value of Z of given confidence interval is,

`(z_(\alpha))/(2)=1.96_{}_{}`

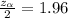
Now,

Find the sample size n;

So,

The formula of the sample size n is,

`n=(((Z_(\alpha))/(2)*\sigma)^2)/(E^2)`

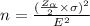
Then,

Put the all given value in above formula,

So,

`\begin{gathered} n=(((Z_(\alpha))/(2)*\sigma)^2)/(E^2) \\ n=\frac{(1.96*0.45)^2}{(0.14)^2^{}} \end{gathered}`

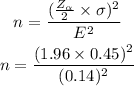
Then,

Find the value of n from above equation;

`\begin{gathered} n=\frac{(1.96*0.45)^2}{(0.14)^2^{}} \\ n=((0.882)^2)/((0.14)^2) \\ n=(0.7779)/(0.0196) \\ n=39.688 \\ n\approx40 \end{gathered}`

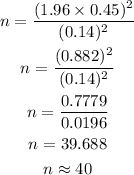
Hence, the pizza shop owner needs $40.