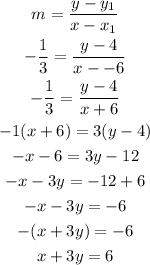Question

Write an equation for the lines that are perpendicular to 6x -2y = 6 and goes through (-6, 4)

Answer 1

x + 3y = 6

Step-by-step explanation

Given equation: 6x - 2y = 6

Expressing the equation given in y = mx + c form will be

2y = 6x - 6

By factorization, we have

2(y) = 2(3x - 3)

y = 3x -3

Gradien m₁ = 3

For the lines perpendicular to 6x - 2y = 6, let the gradient be m₂

Note: For perpendicular lines, m₁m₂ = -1

m₂ = -1/m₁ = -1/3

These lines pass through (-6, 4).

We now use gradient in one point form to determine the equation for the lines as follows

`\begin{gathered} m=(y-y_1)/(x-x_1) \\ -(1)/(3)=(y-4)/(x--6) \\ -(1)/(3)=(y-4)/(x+6) \\ -1(x+6)=3(y-4) \\ -x-6=3y-12 \\ -x-3y=-12+6 \\ -x-3y=-6 \\ -(x+3y)=-6 \\ x+3y=6 \end{gathered}`