Firstly, the equation needs to be balanced.
Let's start by balancing Na, which we can do by adding the coefficient 2 to NaNO₃
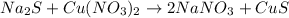
Now, we can check for the other elements.
Cu and S are balanced and the group NO3 is also balanced, so N and O are balanced.
Now, with the balanced equation, we need to consult the molar masses of NaNO₃ and Na₂S, which can be calculated from the molar masses of the elements on them:
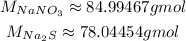
Now, we first convert the mass of NaNO₃ to number of moles:
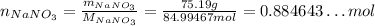
Since the stoichiometry of Na₂S and NaNO₃ is 1 : 2, if we want 0.884643...mol of NaNO₃, we need half as much of Na₂S:
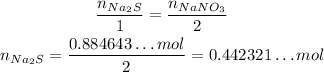
And now, we convert it to mass of Na₂S:
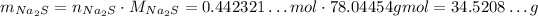
Now, we need to round to 4 significant figures:
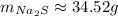
So, the answer is 34.52g of NaNO₃.