Question

Answer ABC c) select the answer that makes the equation trueThanks

Answer 1

ANSWERS

(a)

• Event A:, outcomes: {3, 4, 5, 6, 7, 8}; P(A) = 3/4

,

• Event B:, outcomes: {2, 4, 6, 8}; P(B) = 1/2

,

• Event A or B: ,outcomes: {2, 3, 4, 5, 6, 7, 8}; P(A or B) = 7/8

,

• Event A and B:, outcomes: {4, 6, 8}; P(A and B) = 3/8

(b) 7/8

(c) P(A or B)

Step-by-step explanation

(a) We have an 8-sided die, so there are 8 numbers. The first event, A, is the event where a number greater than 2 is rolled. This is 3, 4, 5, 6, 7, or 8.

If there are 8 numbers in total, then the probability of event A is,

`P(A)=(6)/(8)=(3)/(4)`

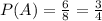
The second event is the event where an even number is rolled. The outcomes are 2, 4, 6, 8, and the probability of event B is,

`P(B)=(4)/(8)=(1)/(2)`

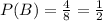
The next event is a combined event, where we want to know the probability that a number greater than 2 is rolled or that an even number is rolled. The outcomes of this event are {2, 3, 4, 5, 6, 7, 8}, which is a combination of the outcomes of events A and B. The probability of this event is,

`P(AorB)=(7)/(8)`

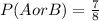
Finally, the last event is where a number greater than 2 and even is rolled. The outcomes of this event are {4, 6, 8}, so the probability is,

`P(AandB)=(3)/(8)`

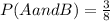
(b) In this part of the problem, we have to compute the given expression replacing the probabilities we found in part (a),

`P(A)+P(B)-P(AandB)=(3)/(4)+(1)/(2)-(3)/(8)=(6)/(8)+(4)/(8)-(3)/(8)=(7)/(8)`

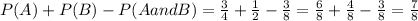
(c) As found in part (b), the result of this expression is the same as P(A or b) that we found in part (a). Hence, the expression is equal to P(A or B).