Question

the trinomial x2 bx c factors to (x m)(x n). if b is negative and c is positive, what must be true about m and n?

Answer 1

Both m and n should be negative

Explanation:

`(x - m)(x - n) = x^(2) -(m + n)x + mn`

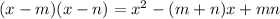
Comparing this with

`x^(2) -bx+c`, we get,

b = m + n and c = mn

We have been given that c should be positive. So, we have two cases:

1. Both m and n should be positive and

2. Both m and n should be negative

Case 1: Both m and n are positive

If both m and n are positive, then so is mn = c.

But, note that m + n (= b) will also be positive. But, it is given that b should be negative. So, this case is not possible.

Case 2: Both m and n are negative

If both m and n are negative, then mn (= c) is positive.

Also, m + n (= b) is negative.

Hence, this is the correct case.

Answer 2

For c to be positive, and for b to be negative, m must be negative and n must be negative.

X^2 - bx + c = (x - m)(x - n).

c is the product of m and n. If both m and n are positive, c would be positive. However b is the sum of m and n, therefore to make b negative, both m and n must be negative to ensure that the product of m and n is positive