Question

A rowing team rowed 100 miles while going with the current in the same amount of time as it took to row 20 miles going against the current. The rate of thecurrent was 6 miles per hour. Find the rate of the rowing team in still water.Rate of the team in still water: (??)miles/hour

Answer 1

By multiplying the time of rowing by the speed we get the distance, like this:

d = S×t

Where d is the distance, S is the speed and t is the time.

When the team is going in the direction of the current their actual speed is the speed of the current plus their still speed, then we can rewrite the above expression to get:

100 = (s + 6)t

Where 100 was the distance the team rowed in miles and 6 is the current rate in miles per hour.

Similarly, when the team goes against the current their actual speed is the still speed minus the speed of the current, then we can rewrite the expression to get:

20 = (s - 6)t

By dividing the first equation by the second one, we get:

`\begin{gathered} (100)/(20)=((s+6)t)/((s-6)t) \\ 5=(s+6)/(s-6) \end{gathered}`

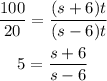
From this expression, we can solve for s to get:

`\begin{gathered} 5=(s+6)/(s-6) \\ 5(s-6)=s+6 \\ 5s-30=s+6 \\ 5s-s-30=s-s+6 \\ 4s-30=6 \\ 4s-30+30=6+30 \\ 4s=36 \\ s=(36)/(4) \\ s=9 \end{gathered}`

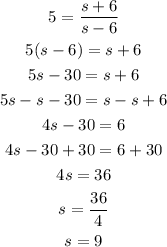
Then, the still speed of the rowing team is 9 miles per hour