Question

a catapult launches a boulder with an upward velocity of 92 m/s. the height of the boulder, h, in meters after t seconds is given by the function h=-5t^2+92t+16. how long does it take to reach maximum height? what is the boulders maximum height?

Answer 1

h = - 5 t² + 92 t + 16
h ` = - 10 t + 92
- 10 t + 92 = 0
10 t = 92
t = 92 : 10
t = 9.2 s
h max = - 5 · 9.2² + 92 · 9.2 + 16 = - 432.2 + 846.6 + 16 = 430.2 m
Answer: It will take 9.2 seconds to reach the maximum height of 430.2 m.

Answer 2

Step-by-step explanation:

It is given that,

Upward velocity of a boulder, v = 92 m/s

The height of the boulder, h, in meters after t seconds is given by the function as :

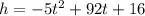`h=-5t^2+92t+16`............(1)

We have to find the time taken by boulder to reach maximum height. For this, we have to differentiate equation (1) w.r.t. t and putting it equal to 0. So,

`(dh)/(dt)=0`

`(d(-5t^2+92t+16))/(dt)=0`

`-10t+92=0`

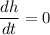
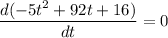
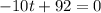
t = 9.2 s

Putting the value of t = 9.2 s in equation (1). So,

`h=-5* (9.2)^2+92* 9.2+16`

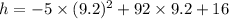
h = 439.2 m

So, the time taken by it to reach maximum height is 9.2 s and the maximum height is 439.2 m. Hence, this is the required solution.