Question

College costs have risen dramatically over the past few decades. For the 2014/2015 school year, the average tuition costs, including room and board, at four-year institutions was $23,600 per year. The standard deviation for those tuition costs was $6,023, and this tuition data seems to follow a normal probability distribution. Find the probability that a randomly selected four-year school has an annual cost between $25,000 and $30,000.

Answer 1

0.2644

Step-by-step explanation

The tuition costs is a random variable X normally distributed with a mean of $23600 and a standard deviation of $6023.

We have to find the probability that a randomly selected college has an annual cost between $25000 and $30000. This is,

`P(25000\lt X\lt30000)`

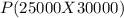
Using the standard normal distribution formula,

`Z=(X-\mu)/(\sigma)`

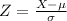
We have,

`P(25000\lt X\lt30000)=P\left((25000-23600)/(6023)\lt(X-\mu)/(\sigma)\lt(30000-23600)/(6023)\right)=P(0.23\lt Z\lt1.06)`

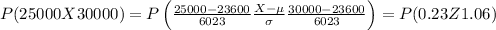
Now, we have to look up these z-values in a z-score table. These tables show the area under the standard normal curve to the left of each z-score - i.e. they show the probability that Z is less than that value. So, to find this probability we have to separate each interval and use a complement,

So we have,

`P(0.23\lt Z\lt1.06)=P(Z\lt1.06)-P(Z\lt0.23)`

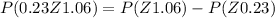
These z-scores in a z-table are,

So the probability is,

`P(25000\lt X\lt30000)=P(Z\lt1.06)-P(Z\lt0.23)=0.8554-0.5910=0.2644`

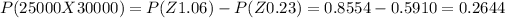
Hence, the probability that a randomly selected college will have an annual cost between $25000 and $30000 is 0.2644.