Width: 5 meters
Length: 7 meters
1) Given that, the area of a rectangle is the product between its length and height.
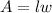
2) Let's write two algebraic expressions for the length and the width according to the text:
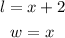
And now, plug them into the Area, like this:
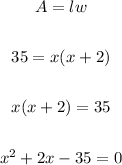
Now, let's solve this quadratic equation to get the quantity of x:
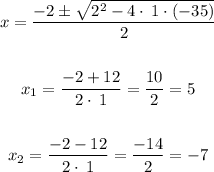
We cannot consider the negative measure for x, since measurements cannot be negative. So now, we can tell that the width is 5 and length is 5+2= 7