Question

D(5, 7), E(4, 3), and F(8, 2) form the vertices of a triangle. What is
m∠DEF?

Answer 1

DE^2 = 1 + 16 = 17.
EF^2 = 16 + 1 = 17.
DF^2 = 9 + 25 = 34.
Since (DE)^2 + (EF)^2 = (DF)^2,
angle E is 90 degrees.
DF must be the hypotenuse
see attachment below

Answer 2

m∠DEF is 90°

Explanation:

It is given that D(5, 7), E(4, 3), and F(8, 2) form the vertices of a triangle. Thus, using the distance formula, we have

`DE=√((3-7)^2+(4-5)^2)`

⇒
`DE=√(16+1)`

⇒
`DE=√(17)`

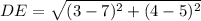
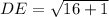
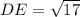
and
`EF=√((2-3)^2+(8-4)^2)`

⇒
`EF=√(1+16)`

⇒
`EF=√(17)`

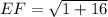
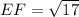
Also,
`DF=√((2-7)^2+(8-6)^2)`

⇒
`DF=√(25+9)`

⇒
`DF=√(34)`

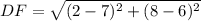
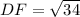
Now,
`(DF)^2=(DE)^2+(EF)^2`

⇒
`(√(34))^2=(√(17))^2+(√(17))^2`

⇒
`34=34`

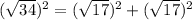
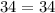
Thus, Pythagoras theorem holds.

Hence, m∠DEF is 90°⇒ΔDEF is right angled triangle which is right angled at E.