Question

What is the logarithmic form of the equation e3x ≈ 3247?

log3x3247 = e

ln 3247 = 3x

3 logxe = 3247

ln 3x = 3247

Answer 1

Option B - ln 3247 = 3x

Explanation:

We have given that : Equation =
`e^(3x) =3247`

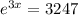
To find : The logarithmic form of the given equation

Solution :
`e^(3x) =3247`

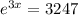
Taking 'ln' both side (ln= natural log)

`ln(e^(3x)) =ln(3247)` .........(1)

∵ Logarithm rule -
`ln(e^x)= x`

∴
`ln(e^(3x))= 3x`

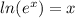
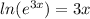
Now we put back in equation (1) we get,

`3x =ln(3247)`

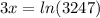
or ln 3247=3x

Therefore, option B is correct

Answer 2

log3x3247 = e
ln 3247 = 3x 3 logxe = 3247

ln 3x = 3247
option B is right
hope this helps