Question

A particle’s position along the x-axis is described by the functionx(t) = A t + B t2,where t is in seconds, x is in meters, and the constants A and B are given below.Randomized VariablesA = -4.9 m/sB = 6.9 m/s2

Answer 1

In order to determine the time when the particle velocity is zero, proceed a follow:

- Calculate the first derivative of the function x(t):

`\begin{gathered} x(t)=At+Bt^2 \\ x^(\prime)(t)=A+2Bt \end{gathered}`

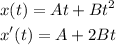
- Next, consider that x'(t) is the velocity of the particle. Then, equal x'(t) to zero and solve for t:

`\begin{gathered} A+2Bt=0 \\ t=-(A)/(2B) \end{gathered}`

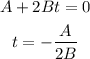
- Next, replace the values A = -4.9m/s and B = 6.9 m/s^2 into the previous expression for t:

`t=-(-4.9(m)/(s))/(2(6.9(m)/(s^2)))=0.35s\approx0.4s`

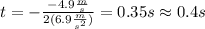
Then, for t approximately equal to 0.4 s the velocity of the particle is zero.