In order to determine the time when the particle velocity is zero, proceed a follow:
- Calculate the first derivative of the function x(t):
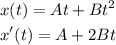
- Next, consider that x'(t) is the velocity of the particle. Then, equal x'(t) to zero and solve for t:

- Next, replace the values A = -4.9m/s and B = 6.9 m/s^2 into the previous expression for t:
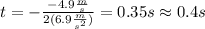
Then, for t approximately equal to 0.4 s the velocity of the particle is zero.