Question

What is the discontinuity of the function f(x)=x^2-3x-28/x+4?

A. (-7,-14)
B. (7,0)
C. (4,-3)
D. (-4,-11)

Answer 1

In case that the equation is f(x)=x^2-3x-28/(x+4)
it has a discontinuity issue in x = -4 due to division by 0

in this case the option would be
D. (-4,-11)

Answer 2

Option D is correct that is (-4,-11).

Explanation:

We have been given an expression:

`f(x)=(x^2-3x-28)/(x+4)`

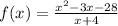
We need to find the points of discontinuity

We will first factorize the given expression

`(x^2-7x+4x-28)/(x+4)`

`\Rightarrow (x(x-7)+4(x-7))/(x+4)`

`\Rightarrow ((x+4)(x-7))/(x+4)`

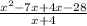
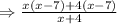
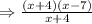
Hence, the point of discontinuity is where denominator gives value zero

So,
`x+4=0\Rightarrow x=-4`

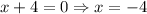
Point of discontinuity is -4

hence, after removing the point of discontinuity the function left is:

`f(x)=x-7`

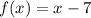
Hence, put x=-4

`f(-4)=-4-7=-11`

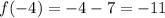
Therefore, option D is correct that is (-4,-11).