Answer: The numbers are 1 and 3.
Explanation:
Let x = smaller number , y= larger number.
As per given,
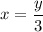 ...(i)
...(i)
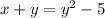 ...(ii)
...(ii)
Put value of x from (i) in (ii)
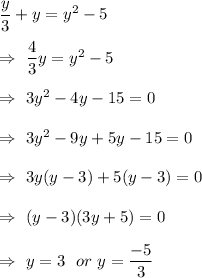
Since numbers are positive , so y=3 is correct.
And x will be 1 [from (i)]
Hence, the numbers are 1 and 3.