Question

What is a quartic function with only the two real zeros given?

x = -4 and x = -1
A. y = x^4 + 5x^3 + 5x^2 + 5x + 4
B. y = x^4 - 5x^3 - 5x^2 - 5x - 4
C. y = -x^4 + 5x^3 + 5x^2 + 5x + 4
D. y = x^4 + 5x^3 + 5x^2 + 5x - 5

Answer 1

A x+4=0 x+1=0 so factores (x+4)(x+1)=0; x^2+5x+4 is a factor. Divide it into x^4+5x^3+5x^2+4 and you get x^2+1 as the other factor which would be your other 2 roots (imaginary)

Answer 2

The correct option is A.

Explanation:

It is given that a quartic function has only two real zeros.

The degree of quartic function is 4. The function has only two real roots, therefore the roots has their multiplicity.

Put -1 and -4 for x. If the value of f(x)=0 at x=-4 and x=-1 then the function have two zeros -4 and -1.

`y = x^4 + 5x^3 + 5x^2 + 5x + 4`

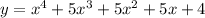
Put x=-1

`y = (-1)^4 + 5(-1)^3 + 5(-1)^2 + 5(-1) + 4=0`

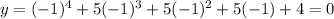
Put x=-4

`y = (-4)^4 + 5(-4)^3 + 5(-4)^2 + 5(-4) + 4=0`

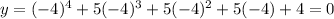
Therefore option A is correct.

`y = x^4 - 5x^3 - 5x^2 - 5x - 4`

The value of y is 2 at x=-1 and 512 at x=-4, therefore option B is incorrect.

`y = -x^4 + 5x^3 + 5x^2 + 5x + 4`

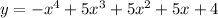
The value of y is -2 at x=-1 and -512 at x=-4, therefore option C is incorrect.

`y = x^4 + 5x^3 + 5x^2 + 5x - 5`

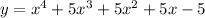
The value of y is -9 at x=-1 and -9 at x=-4, therefore option D is incorrect.