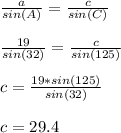Question

Solve the triangle. A = 32°, a = 19, b = 14 (1 point) B = 23°, C = 125°, c ≈17.6 Cannot be solved B = 23°, C = 125°, c ≈29.4 B = 23°, C = 145°, c ≈23.5

Answer 1

B = 23°, C = 125°, c ≈29.4

Explanation:

Answer 2

The answer is below

Explanation:

Given the triangle with: A = 32°, a = 19, b = 14

The sine rule states that for a triangle with lengths of a, b and c and the corresponding angles which are opposite the sides as A, B and C, then the following rule holds:

`(a)/(sinA)=(b)/(sinB)=(c)/(sinC)`

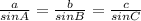
Given, that for triangle ABC; A = 32°, a = 19, b = 14. therefore:

`(a)/(sinA)=(b)/(sinB)\\\\(19)/(sin(32))=(14)/(sin(B))\\\\sin(B)=(14*sin(32))/(19) \\\\sin(B)=0.39\\\\B=sin^(-1)(0.39)\\\\B=23^o`

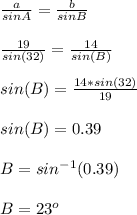
A + B + C = 180° (sum of angles in a triangle)

32 + 23 + C = 180

55 + C = 180

C = 180 - 55

C = 125°

`(a)/(sin(A))=(c)/(sin(C))\\\\(19)/(sin(32))=(c)/(sin(125)) \\\\c=(19*sin(125))/(sin(32)) \\\\c=29.4`