Question

From your home the route to the store that passes the beach is 2 miles shorter than the route to the store that passes the park. What is the length of each route

Answer 1

House to beach + beach to store = house to park + park to store - 2 (x + 2) + (2x + 2) = (4x) + (x) - 2 3x + 4 = 5x - 2 3x + 6 = 5x 6 = 2x x = 3 Check this: (3 + 2) + (2[3] + 2) = (4[3]) + (3) - 2 5 + 8 = 12 + 3 - 2 13 = 13 So the route from home to the beach and the beach to the store is 13 miles, and the route from home to the park and from the park to the store is 15 miles.

Answer 2

The length of first route is 13 units and length of second route is 15 units.

Explanation:

Consider the below diagram has been attached with this question.

Using the below diagram we get

Length of the route from home to the store that passes the beach is

`R_1=(x+2)+(2x+2)=3x+4`

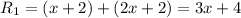
Length of the route from home to the store that passes the park is

`R_2=4x+x=5x`

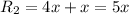
It is given that from your home the route to the store that passes the beach is 2 miles shorter than the route to the store that passes the park.

`R_1=R_2-2`

`3x+4=5x-2`

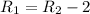
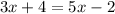
Subtract 5x from both sides.

`-2x+4=-2`

Subtract 4 from both sides.

`-2x=-2-4`

`-2x=-6`

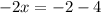
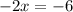
Divide both sides by -2.

`x=3`

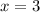
The value of x is 3.

The length of each route is

`R_1=3x+4=3(3)+4=13`

`R_2=5x=5(2)=15`

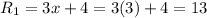
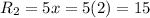
Therefore, the length of first route is 13 units and length of second route is 15 units.