Question

Two 90.0-kilogram people are separated by 3.00 meters. What is the magnitude of the gravitational force that one person exerts on the other?

Answer 1

the magnitude of gravitational force is 6 x 10⁻⁸ N.

Step-by-step explanation:

Given;

mass of the two people, m₁ and m₂ = 90 kg

distance between them, r = 3.0 m

The magnitude of gravitational force exerted by one person on another is calculated as;

`F = (Gm_1m_2)/(r^2) \\\\`

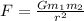
where;

G is gravitational constant = 6.67 x 10⁻¹¹ Nm²/kg²

`F = (Gm_1m_2)/(r^2) \\\\F = (6.67* 10^(-11) * \ 90 \ * \ 90)/(3^2) \\\\F = 6* 10^(-8) \ N`

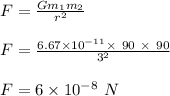
Therefore, the magnitude of gravitational force is 6 x 10⁻⁸ N.