Question

Timothy purchased a computer for $1,000.

The value of the computer depreciates by 20% every year.


This situation represents [a.) exponential decay, b.) exponential growth]


The rate of growth or decay, r, is equal to [c.) 0.8, d.) 1.2, e.)0.2

year.


So the value of the computer each year is [f.) 20 %, g.) 80%, h.) 120%] of the value in the previous year.


It will take [i.) 3, j.) 2, k.) 4, l.) 5.] years for the value of the computer to reach $512.

Answer 1

This situation represents [a.) exponential decay

The rate of growth or decay, r, is equal to c.) 0.2

So the value of the computer each year is g.) 80% of the value in the previous year.

It will take [i.) 3 years for the value of the computer to reach $512.

Explanation:

Since the value depreciates each year, it represents exponential decay.

The rate of growth or decay, r, is equal to

Depreciates 20%, so r = 0.2.

So the value of the computer each year is ... of the value in the previous year,

Depreciates 20%, so it is 100% - 20% = 80% of the value in the previous year.

It will take x years for the value of the computer to reach $512.

The value of the computer after x years is given by:

`V(x) = V(0)(1-r)^x`

In which V(0) is the initial value and r is the decay rate. So

`V(x) = 1000(1-0.2)^x`

`V(x) = 1000(0.8)^x`

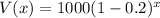
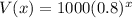
We want to find x for which V(x) = 512. So

`V(x) = 1000(0.8)^x`

`512 = 1000(0.8)^x`

`(0.8)^x = (512)/(1000)`

`(0.8)^x = (0.512)`

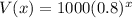
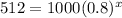
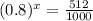
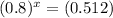
Applying log to both sides:

`\log{(0.8)^x} = \log{(0.512)}`

`x\log{0.8} = \log{(0.512)}`

`x = \frac{\log{0.512}}{\log{0.8}}`

`x = 3`

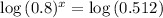
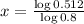
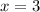
So it will take 3 years.