Question

You are considering two investment opportunities. For investment A there is a 25% chance that you lose $20,000, a 50% chance that you break even, and a 25% chance that you make $80,000. For investment B there is a 30% chance that you lose $50,000, a 50% chance that you break even, and a 20% chance that you make $180,000. Based on the expected value of each, which investment should you make?

Answer 1

a 15000 !!! i just took the question

b 21000

Answer 2

you should make investment B

Explanation:

The expected value of a discrete variable is calculated as:

`E(x)=x_1P(x_1)+x_2P(x_2)+ ... + x_nP(x_n)`

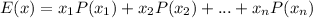
Where
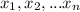`x_1, x_2, ... x_n` are the possible values for the variable and
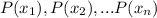`P(x_1), P(x_2), ... P(x_n)` are their respective probabilities.

Then, the expected value for investment A is:

E(A) = -20,000(0.25) + 0(0.5) + 80,000(0.25) = $15,000

Because, you can lose $20,000 with a probability of 0.25, you can break even with a probability of 0.5 or you can win $80,000 with a probability of 0.25.

At the same way, the expected value for investment B is:

E(B) = -50,000(0.3) + 0(0.5) + 180,000(0.2) = $21,000

Then, you should make investment B because the expected value for investment B is bigger than the expected value for investment A.