Question

A ground state hydrogen atom absorbs a photon of light having a wavelength of 92.30 nm. It then gives off a photon having a wavelength of 1820 nm. What is the final state of the hydrogen atom?

Answer 1

n=5

Step-by-step explanation:

We use the Rydberg formula to solve this problem:

1 / λ =
`R_(H)*((1)/(n_(1)^(2))-(1)/(n_(2)^(2)) )`

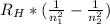
Where λ is the wavelength of absorption/emission, RH is a constant (1.097*10⁷m⁻¹), n₁ is the state of minor energy and n₂ is the state with higher energy.

• First, for the description for the absorption we have λ=92.3 * 10⁻⁹m, and n₁ = 1, so we solve for n₂:

1 / 92.3 * 10⁻⁹m = 1.097*10⁷m⁻¹ *
`((1)/(1^(2))-(1)/(n_(2)^(2))  )`

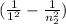
0.988 =
`1-(1)/(n_(2)^(2))`

`(1)/(n_(2)^(2))=0.012\\`

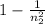
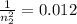
n_{2}^{2}=83.333\\\_{2}=9.12[/tex]

So after absorbing the wavelength of 92.30 nm the state of the hydrogen atom is n=9

• Now for the emission, we have λ=1820 *10⁻⁹m = 1.82*10⁻⁶m, and n₂=9, so we solve for n₁:

`1 / 1.82*10^(-6)m = 1.097*10^(7)m*((1)/(n_(2)^(2))-(1)/(9^(2))  )\\5.009*10^(-2)=(1)/(n_(2)^(2))-(1)/(81)\\(1)/(n_(2)^(2))=0.0377\\n_(2)^(2)=26.50\\n_(2)=5.14`

So the final state of the hydrogen atom is n=5

Answer 2

energy provided=13.4 eV
energy released=0.7 eV
energy absorbed = 12.7eV
initial energy= -13.6eV [ground state]
final energy = -13.6+12.7 = -0.9 eV

This energy corresponds to n=4 in hydrogen atom