Question

The motion of a simple spring hanging from the ceiling can be modeled with a cosine function. The bottom of the spring has a maximum height of 7 feet 4 inches and a minimum height of 6 feet 2 inches from the floor. It takes 2 seconds for the spring to expand from its minimum length to its maximum length. What is a cosine function that models the spring’s length in inches above and below its average, resting position? Express the model as a function of time in seconds

Answer 1

`y = 6'9`

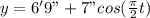
Step-by-step explanation:

As we know that the distance between maximum and minimum distance of the position will be equal to double of the amplitude.

So here we can say that

`2 * Amplitude = maximum\: distance - minimum \:distance`

`2A = 7'4`

`2A = 1'2`

`A = 7 inch`

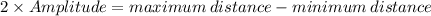
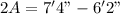
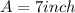
Since it took 2 second to reach the position of maximum length from its position of minimum length so here time period of motion will be

`T = 4 seconds`

so here angular frequency is given as

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(4)`

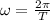
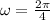
now the equation of motion will be

`y = 6'9`

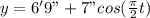
here its mean position from ground is at 6 ft 9 inch above and it will oscillate about it with an amplitude of 7 inch with time period of 4 s

Answer 2

The first step is to substitute the given values in this equation f(x)= A cos (W*t). It is assumed that there is no mass in the resting position. The calculated amplitude is equal to 7. The final answer is f(t) = 7cos(π/2t).