Question

5. Find the area of an equilateral triangle with radius 8 m. Leave your answer in simplest radical form.

Answer 1

The area of an equilateral triangle with a side length of 8 meters is 16\sqrt{3} m², since 'radius' is not a term typically used with equilateral triangles.

Step-by-step explanation:

The question seems to be incorrect as 'radius' is not a term typically associated with an equilateral triangle, rather it is used in the context of circles. However, if we assume that the intention is to find the area of an equilateral triangle with a side length of 8 meters, we can use the formula for the area of an equilateral triangle:

A = (\sqrt{3}/4) × a², where a is the length of a side.

Using the formula and the given side length, the calculation would be:

A = (\sqrt{3}/4) × (8 m)²

A = (\sqrt{3}/4) × 64 m²

A = 16\sqrt{3} m²

This is the area in simplest radical form.

Answer 2

The area of an equilateral triangle is
`83.13m^2`.

Step-by-step explanation:

Given: The radius of an equilateral triangle is 8m.

To find: The area of an equilateral triangle.

Solution: It is given that the radius of an equilateral triangle is 8m.

Now, height of the triangle is given as:

`h=2r`

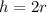
Substituting the value of r, we have

`h=2(8)`

`h=16m`

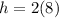
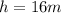
The side of the triangle is given as:

`a=hsin(60^(\circ))`

`a=16(sin60^(\circ))`

`a=16((√(3))/(2))`

`a=8√(3)m`

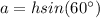
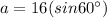
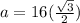
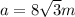
Now, the area of an equilateral triangle is given as:

`Area=(√(3))/(4)(a^2)`

`Area=(√(3))/(4)(8√(3))^2`

`Area=(√(3))/(4){*}64{*}3`

`Arae=48√(3)m^2`

`Area=83.13m^2`

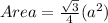
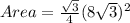
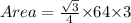
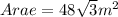
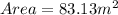
Therefore, the area of an equilateral triangle is
`83.13m^2`.