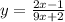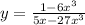Question

Give an example of a rational function that has a horizontal asymptote of y = 2/9..

Answer 1

The horizontal asymptote of a rational function tells us the limiting value of that function as it approaches infinity.

For a rational function to have a horizontal asymptote of

`(2)/(9)`
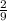
then,


The second condition is that,



Example are given in the graph above.

Here are some other examples,


`y = (2x - 1)/(9x + 2)`



`y = \frac{1 - 6 {x}^(3) }{5x - 27 {x}^(3) }`