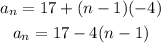ANSWER

Step-by-step explanation
We want to find the formula for the nth term of the sequence given:
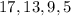
From the sequence, we notice that each successive term is arithmetically less than the preceding term. This implies that the sequence is an arithmetic sequence.
The general formula for an arithmetic sequence is:
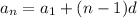
where an = nth term
a1 = first term
d = common difference
The first term for the given sequence is 17.
To find the common difference, find the difference between two successive terms. Let us make use of 13 and 17:
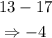
That is the common difference.
Hence, the formula for the nth term of the sequence is: