Answer:
blank = -11
Explanation:
The given function is :
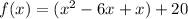
We need to find the number x such that it forms the complete square.
If x = -11, then it will becomes,
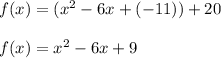
We can write it as follows :
 ..(1)
..(1)
We know that,
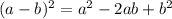 ...(2)
...(2)
Comparing (1) and (2).
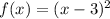
So, if we put the blank equals -11, then it will become the perfect square.