Question

Use the given information to solve for XIn parallelogram ABCD, AE = 3x + 1 and EC = x + 25.

Answer 1

The figure appears to be a parallelogram with diagonals AC and BD with E as the point of intersection of the two diagonals and also the midpoint.

Diagonal AC has segments AE measuring 3x + 1 and EC measuring x + 25. Since point E is the midpoint of the mentioned diagonal, therefore, we can say that the segments AE and EC should be congruent.

We get,

`\text{ AE = EC}`

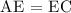
Let's use this relationship to find x.

`\text{ AE = EC}`
`\text{ 3x + 1 = x + 25}`
`\text{ 3x + 1 - x - 1 = x + 25 - x - 1}`
`\text{ 2x = 24}`
`\text{ }\frac{\text{2x}}{2}\text{ = }\frac{\text{24}}{2}`
`\text{ x = 12}`

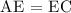
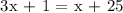
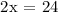
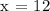
Therefore, x = 12.