Question

A monopoly firm has the following demand and cost conditions:P = 100 -0.5qTC=1000+10q+q²MC = 10 + 2qa. Find the output level q* which maximizes profit

Answer 1

Given P, TC, MC, the profit is given by

`\pi=Pq-TC-MC`

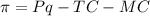
Now, to find the q that maximizes the profit, consider the first and the second derivative of the last function.

`(d)/(dq)\pi=P+q(d)/(dq)P-(d)/(dq)(TC)-(d)/(dq)(MC)=100-0.5q+q(-0.5)-(2q+10)-2`

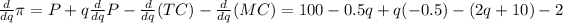
after solving this part we get that

`88-3q=0\text{ will give us the critical points for the profit function.}`

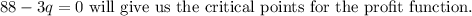
So,

`q=(88)/(3);`

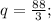
Finally, the second derivative of the profit function gives us

`(d^2)/(dq^2)\pi=(d)/(dq)(88-3q)=-3<0`

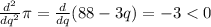
It means that the profit function has a maximum local point at q=88/3.