Given P, TC, MC, the profit is given by
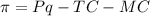
Now, to find the q that maximizes the profit, consider the first and the second derivative of the last function.
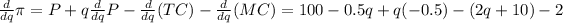
after solving this part we get that
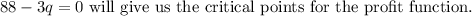
So,
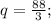
Finally, the second derivative of the profit function gives us
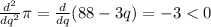
It means that the profit function has a maximum local point at q=88/3.