First, identify the coordinates of the points A, B and C:
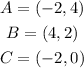
The rule for the transformation of a dilation by a scale factor k is:
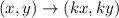
Apply the dilation by a factor of 1/2 to the points A, B and C to find their images A', B', C':
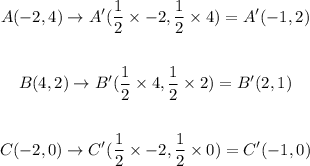
Plot the images A'(-1,2), B'(2,1) and C'(-1,0) to graph the dilation image of the triangle ABC with a scale factor of 1/2: