Answer:
Difference = £10
Explanation:
Represent adult with A and children with C
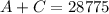
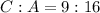
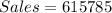
Required
Determine the difference in price of both tickets
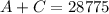
Convert ratio to fraction
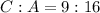
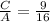
Cross Multiply
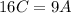
Make C the subject
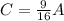
Substitute
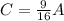 in
in
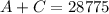
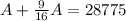
Take LCM


Multiply both sides by 16

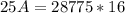
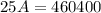
Make A the subject
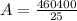
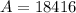
Substitute 18416 for A in
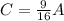
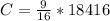
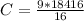
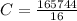
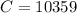
If a children ticket costs £15, then total children tickets cost:
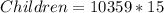
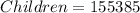
The total sales is given as:
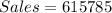
So, the total cost of adult ticket is:
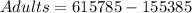
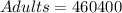
Recall that number of adults is: 18416
So, an adult ticket costs
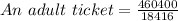

So, we have that:
Children Ticket = £15
Adult Ticket = £25
The difference is:
Difference = £25 - £15
Difference = £10