Question

You are building a new house on a cartesian plane whose units are measured in miles.

Your house is to be located at the point (2,0). Unfortunately, the
existing gas line follows the curve y=√16x2+5x+16.
It costs 400 dollars per mile to install new pipe connecting your house to the existing line.
What is the least amount of money you could pay to get hooked up to the system?

Answer 1

Closest point on the curve y = √(16 x² + 5 x + 16 ) is: ( 0, 4 )
For x =0, y = 4.
Distance from a house:
d = 2² + 4² = 4 + 16 = 20
d = √20 = 4.47213 miles
Costs: 4.47213 x $400 = $1,788.85
The least amount of money to be payed is $1,788.85.

Answer 2

We first find the shortest distance between the point (2, 0) and the curve
`y=√(16x^2+5x+16)`
Let the point on the curve for which the line making the shortest distance be (x, y), then

`d= √((x-2)^2+(y-0)^2) = √((x-2)^2+y^2)`
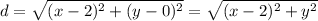
But,
`y=√(16x^2+5x+16)`
Therefore,

`d=\sqrt{(x-2)^2+(√(16x^2+5x+16))^2}=√(x^2-4x+4+16x^2+5x+16)\\= √(17x^2+x+20)`
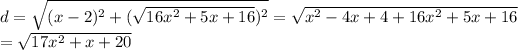
For minimum d(d)/dx = 0

`(d(d))/(dx) = (34x+1)/(2 √(17x^2+x+20)) =0\\34x+1=0\\x=- (1)/(34)`
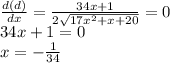
Therefore, shortest distance is

`d= \sqrt{17(- (1)/(34))^2- (1)/(34)+20 } = \sqrt{ (1359)/(68)} =4.47 \ miles`
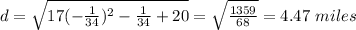
Since it costs 400 dollars per mile, 4.47 miles will cost 4.47 x 400 = $1,788.20