Question

To withstand "g-forces" of up to 10 g's, caused by suddenly pulling out of a steep dive, fighter jet pilots train on a "human centrifuge." 10 g's is an acceleration of 98 m/s2 .

If the length of the centrifuge arm is 12 m , what speed is the rider moving when she experiences 10 g's ?

Answer 1

Centripetal acceleration = speed-squared/radius. /// 98m/s2=speed-squared/12m. ///// 98x12m2/s2=speed^2. ///// Speed=square-root of 98x12=34.3m/s (about 77mph)

Answer 2

When she experiences 10 g's its speed is
`34.293(m)/(s)`

Step-by-step explanation:

I add a graph of the situation.

The centripetal acceleration (in this case 10 g's) is equal to the square of the speed ''V'' divided by the length ''r'' of the centrifuge arm.

`ca=(V^(2))/(r)` (I)

If we replace all the data in the equation (I) :

`98(m)/(s^(2))=(V^(2))/(12m)`

`V^(2)=1176(m^(2))/(s^(2))`

`V=34.293(m)/(s)`

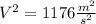
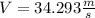
In the graph, I added the centripetal acceleration ''ca'', the acceleration ''a'', the velocity vector ''V'' which magnitude is the speed ''V'' and the tangential acceleration ''ta''.