Question

PLEEASSEEEE Answer ASAP. Due in 5 Minutes. 25 points!!!!!!!!!

Answer 1

Here we will use the relationships:

`a^n*a^m = a^(n + m)`

`(a^n)^m = a^(n*m)`

`(a^n)/(a^m) = a^(n - m)`

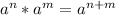
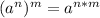
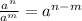
And a number:

`a^n`

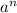
is between 0 and 1 if a is positive and larger than 1, and n is negative.

if a is positive and 0 < a < 1, then we need to have n positive such that:

0 < a^n < 1

A)
`5^3*5^(-4) = 5^(3 + (-4)) = 5^(-1)`

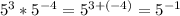
This is between zero and 1,

B)
`(3^5)/(3^(-6)) = 3^(5 - (-6)) = 3^(11)`

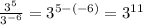
This is greater than 1, because the exponent is positive.

C)
`((1)/(4))^3*( (1)/(4))^2 = ((1)/(4))^(2 + 3) = ((1)/(4))^5`

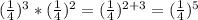
Because a is smaller than 1, and the exponent is positive, then the expression is between 0 and 1.

D)
`((-7)^5)/((-7)^7) = (-7)^(5 - 7) = -7^(-2)`

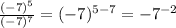
The exponent is negative (and pair) then the expression is between 0 and 1.

Remember that when the exponent is pair, we always have that:

(-N)^m = (N)^m

So (-7)^-2 = 7^-2