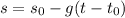Question

A ball is thrown straight up into the air, with an initial speed of 28.2 m/s. How fast is it moving after 1.00 s?

Answer 1

The acceleration of gravity is 9.8 m/s per second. If gravity is
the only force acting on an object and the object is free to move,
then its downward speed grows by 9.8 m/s every second. If it
happens to be moving up, then its upward speed shrinks by 9.8 m/s
every second, until it runs out of upward gas and starts falling.

If the upward speed of the ball is 28.2 m/s at some point in time, then
its upward speed is (28.2 - 9.8) = 18.4 m/s one second later.

Answer 2

After 1.00 sec the speed of the ball will be
`18.4 (m)/(s)`

Step-by-step explanation:

The equation to find the speed at a given time in a vertical thrown is:

`s=s_0-g(t-t_0)`

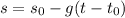
Where
`s_0` is the speed at a time
`t_0`, and
`g` is the accelaration due to gravity.

Then we can calculate the speed of the ball after 1.00 sec replacing the given data:

`s=s_0-g(t-t_0)`

`s_1=28.2 (m)/(s) -9.8 (m)/(s^2) (1 s-0s)`

`s_1=18.4 (m)/(s)`

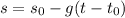
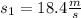
Then, after 1.00 sec the speed of the ball will be
`18.4 (m)/(s)`

The used equation can be found integrating the definition of acceleration as the derivative of speed with respect of time. Like this:

`a=(ds)/(dt)`

`adt=ds`

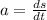
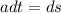
Integrating both sides:

`\int\limits^t_(t_0) {a} \, dt = \int\limits^s_(s_0) {ds}`

`(at) \Big|_(t_0)^t = (s)\Big|_(s_0)^s`

`a(t-t_0)=(s-s_0)`

`s=s_0+a(t-t_0)`

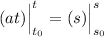
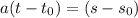
In te case of a vertical thrown,
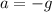`a=-g` so

`s=s_0-g(t-t_0)`