To calculate the five number summary, we need to order the data; the ordered data is:
8, 17, 17, 21, 21, 34, 35, 37, 38, 39, 39, 47, 48
From the ordered data we readily notice that the minimum is 8 and the maximum is 48; now, the median is the central value that divides the set in two, since we have 13 item and this is an odd number the median will be the 7th value of the ordered data, hence the median is 35.
Once we know the median we can calculate the first and third quartiles.
The first quartile is the median of the first half of the data, the first half is:
8, 17, 17, 21, 21, 34
In this case, we have an even number of numbers hence the first quartile will be the mean of the two central values, then:
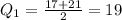
The third quartile is the median of the second half which is:
37, 38, 39, 39, 47, 48
Once again, we have an odd number of items, then the third quartile is the average of the central values:
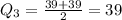
Finally, the interquartile range is defined as the difference of the third and first quartiles:
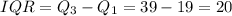
Therefore, we have that:
Minimum 8
Lower quartile 19
Median 35
Upper quartile 39
M