Question

1)What method(s) would you choose to solve the equation:

x2 + 2x - 6 = 0


A. Square roots; there is no x-term.

B. Quadratic formula, graphing; the equation cannot be factored easily since the numbers are large.

C. Factoring; the equation is easily factored.

D. Quadratic formula, completing the square or graphing; the coefficient of x2-term is 1, but the equation cannot be factored.

2)What are the solutions of the equation?
c^2 - 10c = 0


A. 1, – squareroot10

B. 0, –10

C. 0, sqrt10

D. 0, 10

Answer 1

1.

Option D is correct

Quadratic formula, completing the square or graphing; the coefficient of x2-term is 1, but the equation cannot be factored.

2.

Option D is correct

The solutions of the equations are:

c = 0 and c = 10

Explanation:

A quadratic equation is in the form of:

`ax^2+bx+c = 0` ....[1] , the the solution is given by:

`x = (-b \pm √(b^2-4ac))/(2a)`

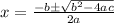
1.

Given the equation:

`x^2 + 2x -6 = 0`

On comparing with [1] we have;

a = 1, b =2 and c = -6

then;

`x = (-2 \pm √((2)^2-4(1)(-6)))/(2(1)) = (-2 \pm √(28))/(2)`

⇒
`x = (-2 \pm 2√(7) )/(2) = -1 \pm √(7)`

⇒
`x = -1+√(7), -1-√(7)`

therefore, the method(s) would you choose to solve the given equation is, Quadratic formula, completing the square or graphing; the coefficient of x2-term is 1, but the equation cannot be factored.

2.

Given the equation:

`c^2-10c = 0`

⇒
`c(c-10) = 0`

By zero product property we have;

`c= 0` and c-10 = 0

⇒c = 0 and c= 10

Therefore, the solutions of the given equation are : 0 and 10

Answer 2

1 )
x² + 2 x - 6 = 0
( x² + 2 x + 1 )- 1 - 6 = 0
( x + 1 )² = 7 /√
x + 1 = +/- √7
x 1 = - 1 + √ 7 ; x 2 = - 1 - √ 7
Answer: D ) Quadratic formula, completing the square or graphing; the coefficient of x² term is 1, but the equation cannot be factored.
2 )
c² - 10 c = 0
c ( c - 10 ) = 0
c = 0; c = 10
Answer: D ) 0, 10