Question

Express the complex number in trigonometric form.

6 - 6i

Answer 1

`8.48(\cos (45)-i\sin (45))`

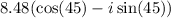
Explanation:

We are given the complex number,
`z=6-6i`.

Now, the trigonometric form of a complex number
`z=a+ib` is given by,
`|z|(\cos \theta+i\sin \theta)`.

Since, we have that,
`|z|=\sqrt{a^(2)+b^(2)}`

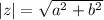
So,
`|z|=\sqrt{6^(2)+(-6)^(2)}`

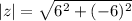
i.e.
`|z|=√(36+36)`

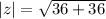
i.e.
`|z|=√(72)`

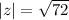
i.e.
`|z|=8.48`

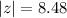
Further, we have that,
`\theta = \arctan((b)/(a))`

So,
`\theta = \arctan((-6)/(6))`

i.e.
`\theta = \arctan(-1)`

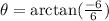
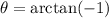
i.e. θ = - 45°

So, the trigonometric form of the given complex number is,

`8.48(\cos (-45)+i\sin (-45))` i.e.
`8.48(\cos (45)-i\sin (45))`

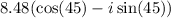
Hence, the trigonometric form is
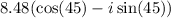`8.48(\cos (45)-i\sin (45))`.

Answer 2

z=6-6i = 6(1-i)
r=
`√(2)`
alpha = arctg(-1)+2pi=7pi/4
z = 6
`√(2)`(cos7pi/4 + i sin 7pi/4)

I hope that this is the answer that you were looking for and it has helped you.