Considering that the angle 5π/4 is a central angle, we have the following sketch representing the question:
Then, to find the length of the intercepted arc (length x), we can use the following rule of three, knowing that the length of the whole circumference (angle of 2π) is equal to 2πr:
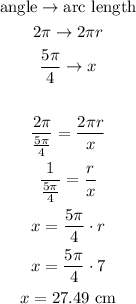
Rounding to the nearest tenth, we have an arc length of 27.5 cm.