Given:
The system of equations:
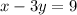
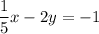
To find:
The number that can be multiplied by the second equation to eliminate the x-variable when the equations are added together.
Solution:
We have,
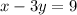...(i)
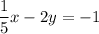...(ii)
The coefficient of x in (i) and (ii) are 1 and
respectively.
To eliminate the variable x by adding the equations, we need the coefficients of x as the additive inverse of each other, i.e, a and -a So, a+(-a)=0.
It means, we have to convert
into -1. It is possible if we multiply the equation (ii) by -5.
On multiplying equation (ii) by -5, we get
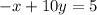...(iii)
On adding (i) and (iii), we get
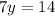
Here, x is eliminated.
Therefore, the number -5 can be multiplied by the second equation to eliminate the x-variable.